This data structure is an important one to know. A Binary Search Tree allows you to maintain a data set in sorted order. This in turn allows you efficiently locate data items. If you would were to use a standard array you would need to sort it every time you add a new data item. Not so with the BST. So with this in mind it must be pretty tricky to implement one, yes? It’s actually quite straightforward. Let us dive in.
Each node in the BST holds some data which can be compared. This is important because it is this that enables data to be chunked or grouped based on the notion that one node is greater than the other.
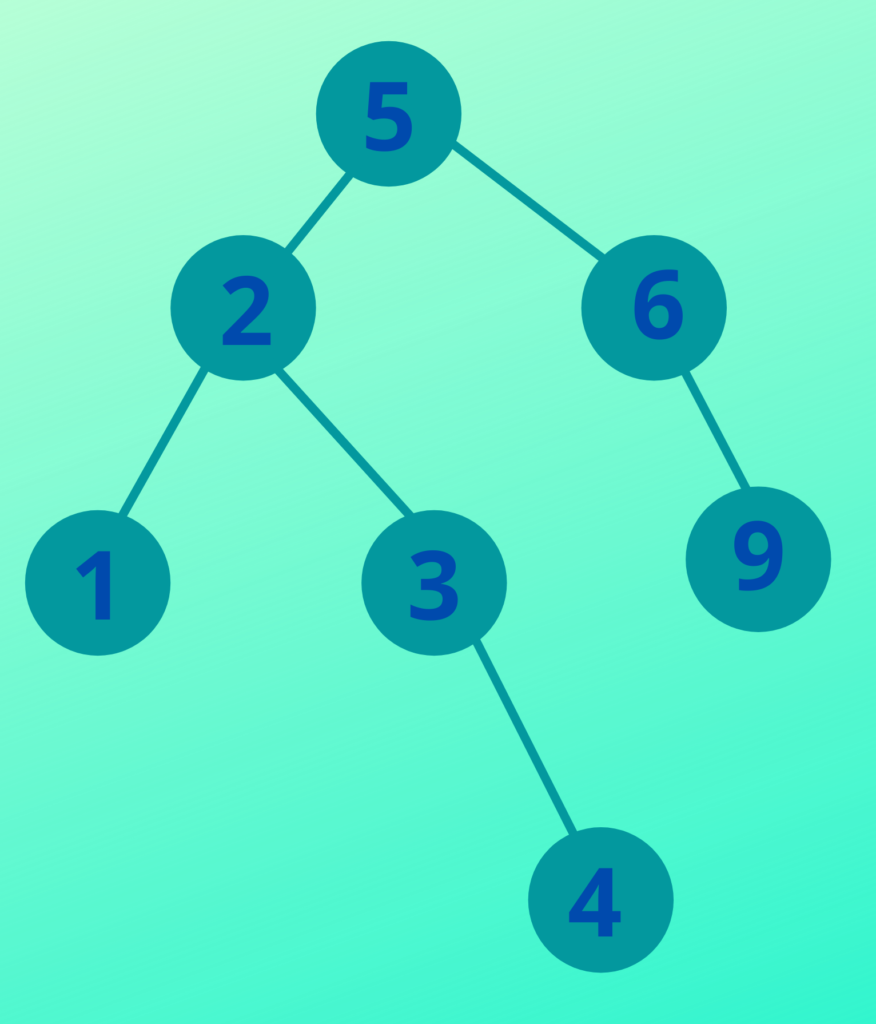
Our data set looks like this 5,2,6,9,1,3,4.
In the example above 5 is the first item to be added. There is nothing in the tree to start with so the root contains 5. Next up in our list is 2. We would examine the first(root) node and ask ourselves this question “Is our new value greater or less than the current node?”. Here 2 is less than 5 so it is placed in the left-hand side of the root node. Next up is 6. Again we would look at the first node(the root) and determine that 6 is greater than 5 and therefore place it in the right-hand side of the root node. Now our root node has two children 2 and 6. Now if we want to add the value 9 we look at the root, 9 is greater than 5 so we will place it on the right-hand side. However we can’t do this because it already has the value 6. Now we look at node containing 6. 9 is greater than 6 so 9 is placed in the right-hand side of the node that contains 6, and so on…
Using this information we can define a Java class to represent a node in a BST.
public class BSTNode {
public int data;
public left;
public right;
public BSTNode(int value) {
data = value;
left = null;
right = null;
}
}The BSTNode class is very simple. It has three public members. One to hold the data, in this case to keep things easy it is just an integer number for easy comparison. The other two hold the left and right child nodes. When the class is constructed the data value is passed in and set. Now to create the tree class itself and a method to add a value to the tree.
public class BinarySearchTree {
public BSTNode root;
public BinarySearchTree() {
root = null;
}
/**
* Add a new node
* @param value The node value
* @return The new node
*/
public BSTNode add(int value) {
// Create the new node
BSTNode newNode = new BSTNode(value);
// If there is no root then create and return
if (this.root == null) {
this.root = newNode;
return this.root;
}
//Recurse through the tree and find the one where the data should be set
BSTNode node = nextNode(this.root, value);
if (value < node.data) {
node.left = newNode;
}
else {
node.right = newNode;
}
return newNode;
}
/**
* Get the next node that has does not have children
* @param node The current node
* @param value The value to be compared against the node's data value
* @return The node
*/
private BSTNode nextNode(BSTNode node, int value) {
boolean leftNode = value < node.data;
if (leftNode && node.left != null) {
return nextNode(node.left, value);
} else if (!leftNode && node.right != null) {
return nextNode(node.right, value);
}
return node;
}
}
In order to effectively traverse the tree I have implemented a recursive function which drills down into each child comparing the value as it goes and when it find the last correct node that does not have left/right child node it returns. The calling function then sets the correct class member left or right depending on the value.
Let’s test our BST. We are going to add a unit test to ensure that the tree has been built correctly.
import static org.junit.Assert.*;
import org.junit.Test;
public class TestBinarySearchTree {
@Test
public void testAdd() {
// 5,2,6,9,1,3,4
BinarySearchTree tree = new BinarySearchTree();
// Add the root 5
BSTNode root = tree.add(5);
assertEquals(root, tree.root);
// Add 2
BSTNode node2 = tree.add(2);
assertEquals(root.left, node2);
// Add 6
BSTNode node6 = tree.add(6);
assertEquals(root.right, node6);
// Add 9
BSTNode node9 = tree.add(9);
assertEquals(node6.right, node9);
// Add 1
BSTNode node1 = tree.add(1);
assertEquals(node2.left, node1);
// Add 3
BSTNode node3 = tree.add(3);
assertEquals(node2.right, node3);
// Add 4
BSTNode node4 = tree.add(4);
assertEquals(node3.right, node4);
}
}Here we are checking that each node is placed correctly in the tree.
